Merkle tree structure
-
 by ZKE Research
by ZKE Research

Merkle tree (also known as a hash tree) is a typical binary tree structure consisting of a root node, a set of intermediate nodes and a set of leaf nodes. The Merkle tree was first proposed by Merkle Ralf in 1980 and has been widely used in file systems and P2P systems.
Its main features are:
The bottommost leaf node contains stored data or its hash;
Non-leaf nodes (including intermediate nodes and root nodes) are the hash values of the contents of its two child nodes.
Further, the Merkle tree can be extended to the case of a multi-fork tree, at this time, the contents of the non-leaf nodes are the hash values of the contents of all its child nodes.
The Merkle tree records the hash value layer by layer, giving it some unique properties. For example, any change in the underlying data will be passed to its parent node, layer by layer along the path to the root of the tree. This means that the value at the root of the tree actually represents a “numerical digest” of all the underlying data.
Currently, typical application scenarios of Merkle trees include the following:
Prove the existence or non-existence of an element in a set
By constructing the Merkle tree of the collection and providing the Hash values in sibling nodes at all levels of the element, it is possible to prove the existence of an element without exposing the complete content of the collection.
In addition, for a collection that can be sorted, you can replace the position where there is no element with a null value to construct a sparse Merkle tree (Sparse Merkle Tree). This structure can prove that a specified element is not included in a set.
Quickly compare large amounts of data
After sorting each set of data, a Merkle tree structure is constructed. When the roots of two Merkle trees are the same, it means that the two sets of data represented must be the same. Otherwise, it must be different.
Since the Hash calculation process can be very fast, the preprocessing can be completed in a short time. Utilizing the Merkle tree structure can bring huge comparative performance advantages.
Quick positioning modification
Take the following figure as an example, construct a Merkle tree based on data D0…D3, if the data in D1 is modified, it will affect N1, N4 and Root.
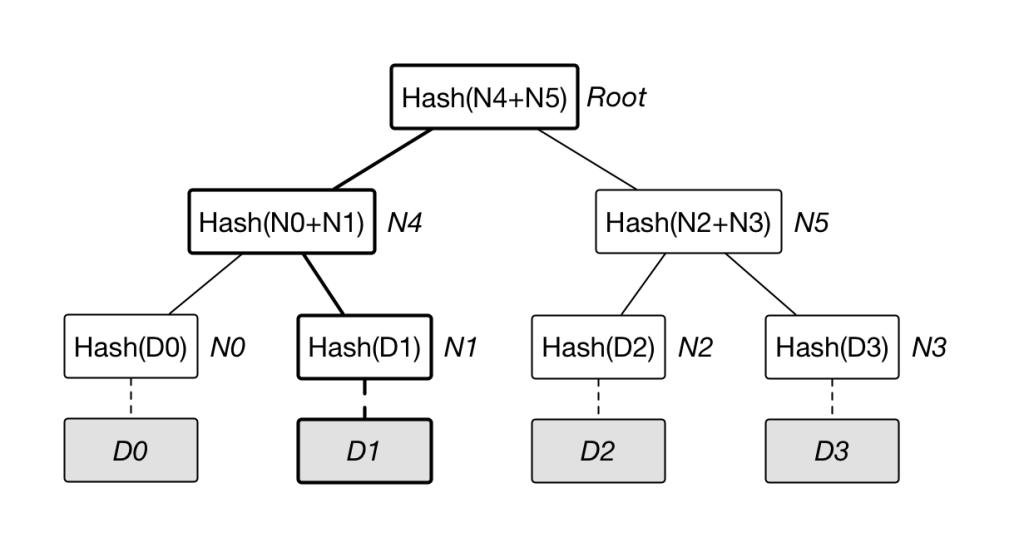
Therefore, once the value of a node such as Root is found to have changed, along Root –> N4 –> N1, the data block D1 that actually changed can be quickly located in O(lgN) time at most.
Zero-knowledge proof
Still taking the above picture as an example, how to prove to others that you own a certain data D0 without revealing other information. The challenger provides random data D1, D2 and D3, or is generated by the prover (need to add specific information to avoid being reused in the proof process).
The prover constructs the Merkle tree as shown in the figure, and announces N1, N5, Root. The verifier can easily detect the existence of D0 by calculating the Root value by itself and verifying whether it is consistent with the provided value. During the whole process, the verifier cannot obtain additional information related to D0.
Merkle tree (also known as a hash tree) is a typical bi…
